我们常有这样的困扰:
“怎样系统地思考一个算法问题?”
“为什么我只会解决见过的算法题,对陌生的算法题不知道怎样着手?”
之所以说传统算法问题,是为了区别于机器学习算法,我们这里所说的算法,只涉及传统的数据结构与算法。
《算法(第4版)》在第一章就解决了这个新手的困扰,介绍思考任意传统算法问题的科学思路。本文做一个梳理,通过Union-find算法作为例子,总结面对一个传统算法场景的思考方向。
总体思路
定义基本操作API -> 定义测试用例 -> 实现一个简单方案 -> 分析算法效率 -> 优化迭代
以 Union-Find 问题为例:
什么是 Union-Find 问题?
假如有很多点,构成这样的集合。
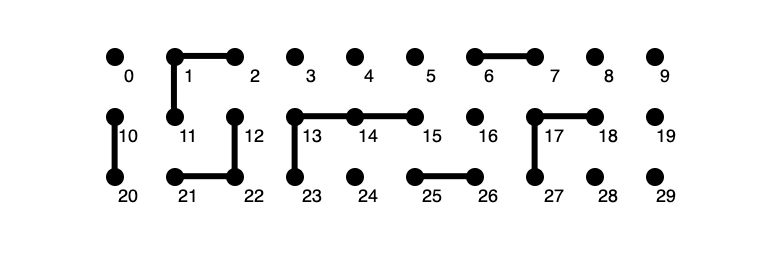
每个点右下角是角标,代表点的位置。
简单来说问题就是判断其中任意2个点是否连接,具体如下:
1. 输入一串数字,每两个数字为一组,比如 tinyUF.txt:
» cat tinyUF.txt
15
4 3
3 8
6 5
9 4
2 1
8 9
5 0
7 2
6 1
1 0
6 7
第一个数字表示数据集合大小,只用来方便测试,我们先忽略它。
2. 从第二行开始每次读2个数字为一组,判断这两个数字代表的点是否连接。(这里定义的连接可以传递,比如a连接b,b连接c,那么a与c也连接。)
3. 如果不连接,实现算法让其连接;如果连接,返回true,然后继续读下一组数。
Step 1. 定义API
一般来讲,我们要先把问题明确为一个函数,规定入参和出参。或者,把问题明确为一个类,规定类中包括哪些成员变量和方法。
当我们想好函数的入参和出参(或这个类的每个方法参数和返回值),就相当于明确了我们要解决什么问题。
这样用“封装”的思想,把问题定义在这个函数或类里,我们只需要思考怎么实现函数就行了。
(据我观察,工作中遇到的很多问题,都是因为没把问题本身想清楚,当你明确了问题之后,问题自然解决了。)
定义 API 就是抽象问题的过程
- 用 int[] 表示所有点的集合。
这相当于把每个点抽象成数组里的一个元素,元素的角标用来确定这个点的位置,元素的值代表这个点的某种信息,比如所在分量的标识。 - 把互相连接的点的集合称为分量。
- 接下来定义解决这个问题的类:
class UF{
// 所有点的集合
private int[] id;
// 分量数量
private int count;
// 初始化
public UF(int N) { }
// 查找分量标识符
public int find(int p) { }
// 两个触点是否连接,也就是是否在同一个分量
public boolean connected(int p, int q) { }
// 连接两个触点
public void union(int p, int q){ }
public int count() { }
}
我们接下来的任务就是实现这个类里面每个方法。 其实,我们只需要优化这两个方法:
//根据角标找到这个点的值
public int find(int p) {}
//连接两个点,参数为角标
public void union(int p, int q) {}
因为其他方法可以基于这两个方法实现。
为了之后方便定义多种实现,把上面的类改为抽象类,同时先实现其他方法的逻辑:
public abstract class UF {
// 所有点的集合
private int[] id;
// 分量数量
private int count;
// 初始化
public UF(int N) {
count = N;
id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
}
// 查找分量标识符
abstract int find(int p);
// 两个点是否连接,也就是是否在同一个分量
public boolean connected(int p, int q) {
return find(p) == find(q);
}
//todo 连接两个点,需要在接下来实现
abstract public void union(int p, int q);
public int count() {
return count;
}
}
这样,之后每次写出新的实现,只需继承同一个抽象类 UF,实现 find() 和 union()。
Step 2. 定义测试用例
在真正写实现逻辑之前,首先写测试代码是比较好的习惯。这既能检测上面定义的API是否合理,也可以方便验证效果。
定义一个实现类,用来写具体逻辑:
public class UFQuickFind extends UF {
// 具体需要实现的方法
public UFQuickFind(int N) {
super(N);
}
// 查找分量标识符
public int find(int p) {
return id[p];
}
//具体需要实现的方法
public void union(int p, int q) {}
//测试用例
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int count = scanner.nextInt();
UFQuickFind qf = new UFQuickFind(count);
while (scanner.hasNextInt()) {
int p = scanner.nextInt();
int q = scanner.nextInt();
// 判断是否连接
if (qf.connected(p, q)) {
continue;
}
// 如果没连接,则归并分量
qf.union(p, q);
// 打印连接
System.out.println(p + " " + q);
}
System.out.println(qf.count() + "components");
}
}
做这种小实验,个人喜欢摆脱 IDE,用命令行编译:
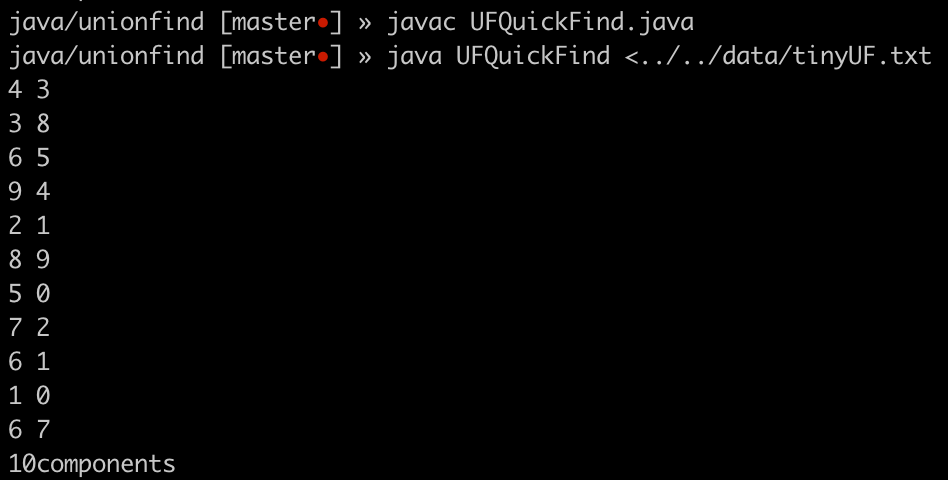
测试数据 tinyUF.txt 可以在《算法》官网找到 https://algs4.cs.princeton.edu/15uf/
Step 3. 简单实现:quick-find 算法
首先我们需要先定义,什么叫连接? 我们姑且用两个元素的值相等来代表连接。显然,同一个分量中每个元素值都相等。 比如:
id[0] == id[5]
代表0和5连接,也就是说属于同一分量。
实现 find() 方法:
上面在 UFQuickFind 类中已经写了这种 find() 方法,很简单,就是拿到数组角标对应的值,代表所属分量。
public int find(int p) {
return id[p];
}
实现 union() 方法:
union() 方法用来连接两个点,只需要遍历每个元素,把一个点所属分量合并到另一个点所属的分量。
public void union(int p, int q) {
// 找p和q各自所属分量
int pGroup = find(p);
int qGroup = find(q);
if (pGroup == qGroup) {
return;
}
// 遍历所有元素,把与q同一个分量的元素放到p所属的分量
for (int t = 0; t < id.length; t++) {
if (id[t] == qGroup) {
id[t] = pGroup;
}
}
count--;
}
因为这个算法的 find() 查找很快,所以叫 quick-find 算法。
测试结果:
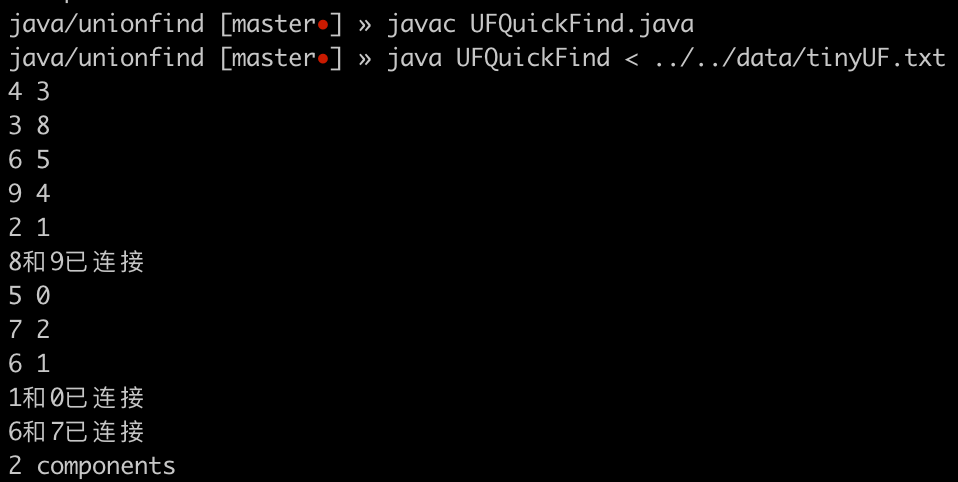
Step 4. 分析效率
显然,quick-find 算法效率不高:
我们在这里把访问数组的次数作为衡量效率的指标,如果不管数据规模如何,某个算法只需访问数组常数次,则复杂度O(1)。这样规定指标的做法叫成本模型,本文这个算法问题的成本模型是访问数组的次数。
- find() 时间复杂度 O(1)
- union() 时间复杂度 O(N),N就是数组长度
- 如果想用 quick-find 算法把所有数据连通,最后只剩下一个分量,最坏情况需要调用 N-1次 union(),那么很明显,这种情况下,时间复杂度 O(N^2)。
对于这个算法,靠直觉就能发现 union() 之所以效率低,是因为遍历了所有元素,受原始数据规模影响。接下来的优化思路,自然是想办法避免这种遍历。
Step 5. 优化:quick-union 算法
如果让一个分量的元素之间构成某种关联关系,能不能避免遍历所有数据?
比如让元素的值来指向另一个元素:
规定id[] 数组每个元素的值是同分量另一个元素的角标
这样,我们根据某个元素,可以追溯同分量的另一个元素,直到最后一个元素,这时,规定最后一个元素的值等于自己的角标。
这样,相当于每个元素的值都像一个“指针”,指向另一个元素。最后一个元素的“指针”指向自己。
想象一下,每个分量构成一个树状结构。
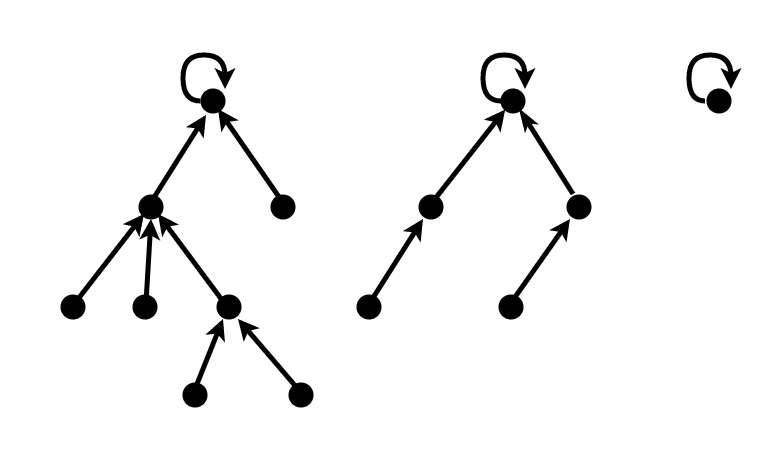
这种设计下,怎么表示两个点“连接”?
显然,当两个点属于同一分量,那么两个点属于同一个“树”,有同一个“根节点”。所以可以用根节点的值表示所属分量,也就是 find() 的返回值。
实现 find()
根据参数角标,拿到对应元素值,指向了下一个元素角标,然后访问下一个元素的值,就是下下个元素角标……不断向前追溯,直到某个元素的值等于自己角标值,说明这个元素是根节点。
我写了两种 find() 方法,一种是递归:
public int find(int p) {
int pVal = id[p];
if (pVal == p) {
return p;
}
return find(pVal);
}
一种用 while() 循环:
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
实现 union()
用 find() 找到两个点各自所属的树的根节点,把一个根节点指向另一个根节点,这样,就合并两个树。
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
id[pRoot] = qRoot;
count--;
return;
}
因为这种算法的 union() 效率很高,所以叫 quick-union 算法。
重复 Step 4 - Step 5 (分析效率 -> 优化算法 -> 分析效率 -> 优化算法……)
分析 quick-union 效率
find() 方法时间复杂度
只看用 while 循环的方法。find() 查找速度受节点与根节点距离(也就是深度)影响,如果节点的父节点就是根节点,那么显然只需要访问数组2次。但如果整个原始数据构成一张树,且节点深度等于 N-1,这是 find() 遇到的最坏情况,如图:
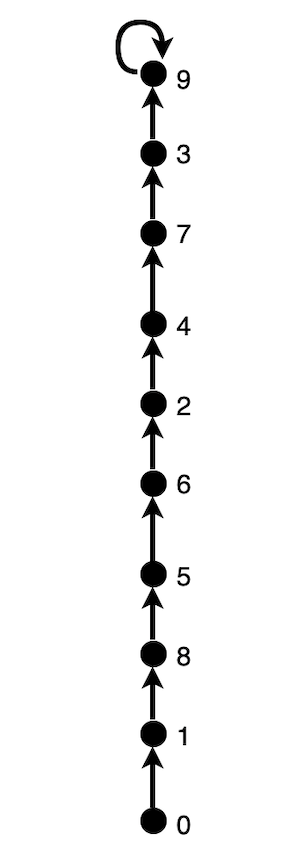
如果调用find(0),则需要访问 2 * (N-1) (每次 while 循环访问2次)。
什么样的输入会导致这种最坏情况?
比如在输入:
0-1 0-2 0-3 0-4 0-5 0-6 0-7 0-8 0-9
这样的序列,find()复杂度为 O(N),union中会调用2次 find(),复杂度也是 O(N)。
如果想把所有元素连通,最坏情况总的复杂度依然是 O(N^2)。
之所以会有这样的情况,是因为每次连接两个树,总是朝固定的一侧合并根节点,可能让本就比较高的树更高,不能限制树的规模。所以接下来思考方向是,怎么控制合并的树的规模,尽量均匀分配,不形成“一棵独大”的树。
继续优化 quick-union 算法:weighted-quick-union 算法
既然我们想控制树的高度(也就是节点中的最大深度),就需要先思考这个问题:树的高度是什么时候增加的?
答案是 union() 中把树 A 根节点指向树 B 根节点的时候,树 A 的高度增加1,树 B 的高度不变。
于是优化的方法呼之欲出:union() 每次合并树的时候,都把高度小的树往高度大的树上合并。使得合并后只增高小树。
我们可以定义一个数组记录根节点对应的树的高度。合并树的时候,读取两个根节点对应的树的高度,找出哪棵树更高:
private int[] height;
//构造方法中初始化 height
public UFWeightedQuickUnion(int N) {
count = N;
id = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
height = new int[N];
for (int i = 0; i < N; i++) {
height[i] = i;
}
}
union() 方法:
void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
int pH = height[pRoot];
int qH = height[qRoot];
if (pH > qH) {
id[qRoot] = pRoot;
height[pRoot]++;
} else {
id[pRoot] = qRoot;
height[qRoot]++;
}
count--;
return;
}
因为这种算法通过记录树的高度作为一种加权(weight),控制合并方向,所以可以叫加权quick-union 算法。
如果不用树的高度作为加权,而是用树的大小,也就是节点数做加权呢?这也是一种加权方法,这里就不介绍了。
分析 weighted-quick-union 算法
- find() 方法复杂度 O(lgN)
- union() 方法复杂度 O(lgN)
- 如果要把所有点合到一个分量,最坏情况的复杂度 O((N -1) * lgN) ~ O(N * lgN)
最优算法:路径压缩 weighted-quick-union 算法
虽然加权 quick-union 算法已经把树的高度控制在 lgN,但毕竟 find() 中追溯根节点的时候还是需要经过其他节点。数据规模越大,节点深度越大,路径越长,如果能缩短这条路径,显然就能大大提升 find() 效率。
干脆让每个节点指向根节点好了。
在 find() 中,找到根节点后,再把路径上每个节点都指向根节点,不就减少树高度了吗?
int find(int p) {
int start = p;
// 让 p 取到根节点的值
while (p != id[p]) {
p = id[p];
}
// 重新遍历,把路径上的节点都指向根节点
while (start != p) {
int temp = start;
start = id[start];
id[temp] = p;
}
return p;
}
分析路径压缩 weighted-quick-union 算法
表面上看压缩路径算法的 find() 中加了一个 while 循环,好像反而增加了复杂度。
可换个角度思考,当树慢慢扩大的时候,高度却没有增加。这样避免了速度受数据规模影响太大。虽然表面上看增加了一个循环,但如果大多数情况节点深度只有2,while 循环也不过只有2次而已。
前面分析时间复杂度都是考虑最坏情况,实际上均摊成本也很重要。路径压缩加权 quick-union 算法均摊成本已经非常接近常数了。具体可以参考《算法(第四版)》,不过书里也只是粗略的介绍这个概念,在我看来不够严谨,以后如果有时间可以进一步分析这个问题。
